Упрощенная HTML-версия
n
n
D(X) = X Pi [xi - M(X)] 2
(1.4)
i
=1
Среднее квадратичное отклонение случайной величины определяется как корень квадратный
из дисперсии.
Определение этих характеристик производится из представления закона распределения
дискретной случайной величины, в котором представлены значения случайной величины -
xi
и их
соответствующие вероятности -
Pi.
Для непрерывной случайной величины весь диапазон измеренных значений от xmin до xmax
делят на определенное число равных интервалов. Затем определяют середину каждого интервала
<x>
и вероятность попадания измеренных значений в каждый интервал:
где
n -
число всех измеренных значений,
mi -
число значений, попадающий в каждый интервал.
Определение характеристик непрерывной случайной величины производится по тем же
формулам, что и для дискретной.
Представление всех значений <xj> и Pi и выражает закон распределения непрерывной
случайной величины.
Закон распределения случайной величины может быть задан в виде таблицы, графически и
аналитически (в виде формулы).
Для графического представления распределений используют главным образом два способа.
1.
Построение полигона (точечной диаграммы). Для этого в системе координат
xi, Pi
отмечают расчетные точки (середины интервалов) и соединяют их прямыми (линия
а
на рисунке 1)
или сглаженными линиями (линия
б
на рисунке 1).
2.
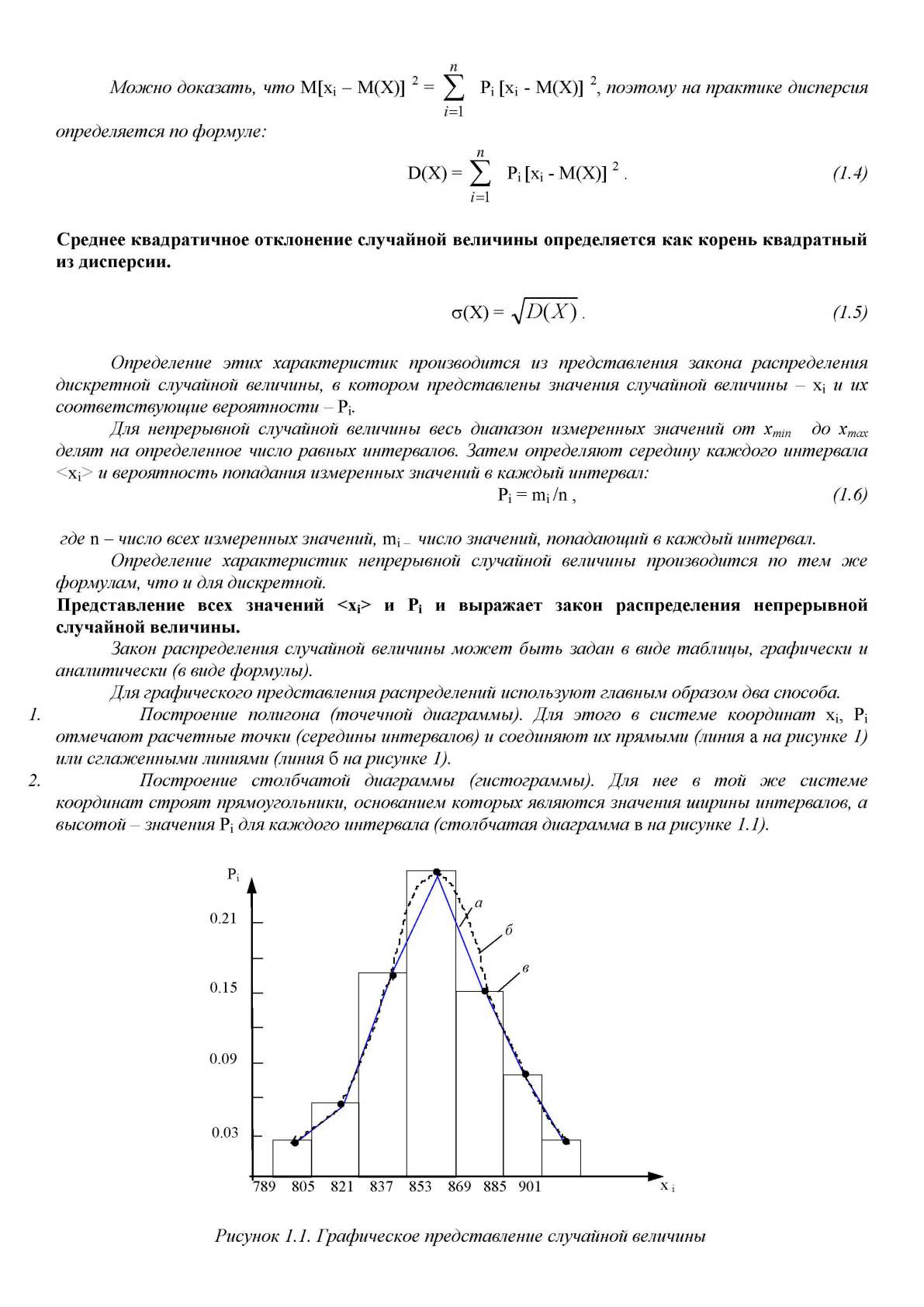
Построение столбчатой диаграммы (гистограммы). Для нее в той же системе
координат строят прямоугольники, основанием которых являются значения ширины интервалов, а
высотой - значения
Pi
для каждого интервала (столбчатая диаграмма
в
на рисунке 1.1).
(1.5)
Pi = mi /n ,
(1.6)
789 805 821 837 853 869 885 901
Рисунок 1.1. Графическое представление случайной величины

