Упрощенная HTML-версия
Электрические свойства диполя характеризуются электрическим
дипольным моментом.
Электрический момент диполя равен произведению модуля одного из электрических зарядов
диполя на вектор l
, проведенный от отрицательного заряда диполя к положительному (рис. 16.2)
(также направлен и вектор дипольного момента):
p
=|
q f
-
Единицей измерения электрического момента диполя является кулон-метр (Кл-м).
По принципу суперпозиции 16.2, и его следствию 16.6 напряженность (потенциал) поля диполя
равна (равен) сумме напряженностей (потенциалов) полей, создаваемых каждым из зарядов диполя.
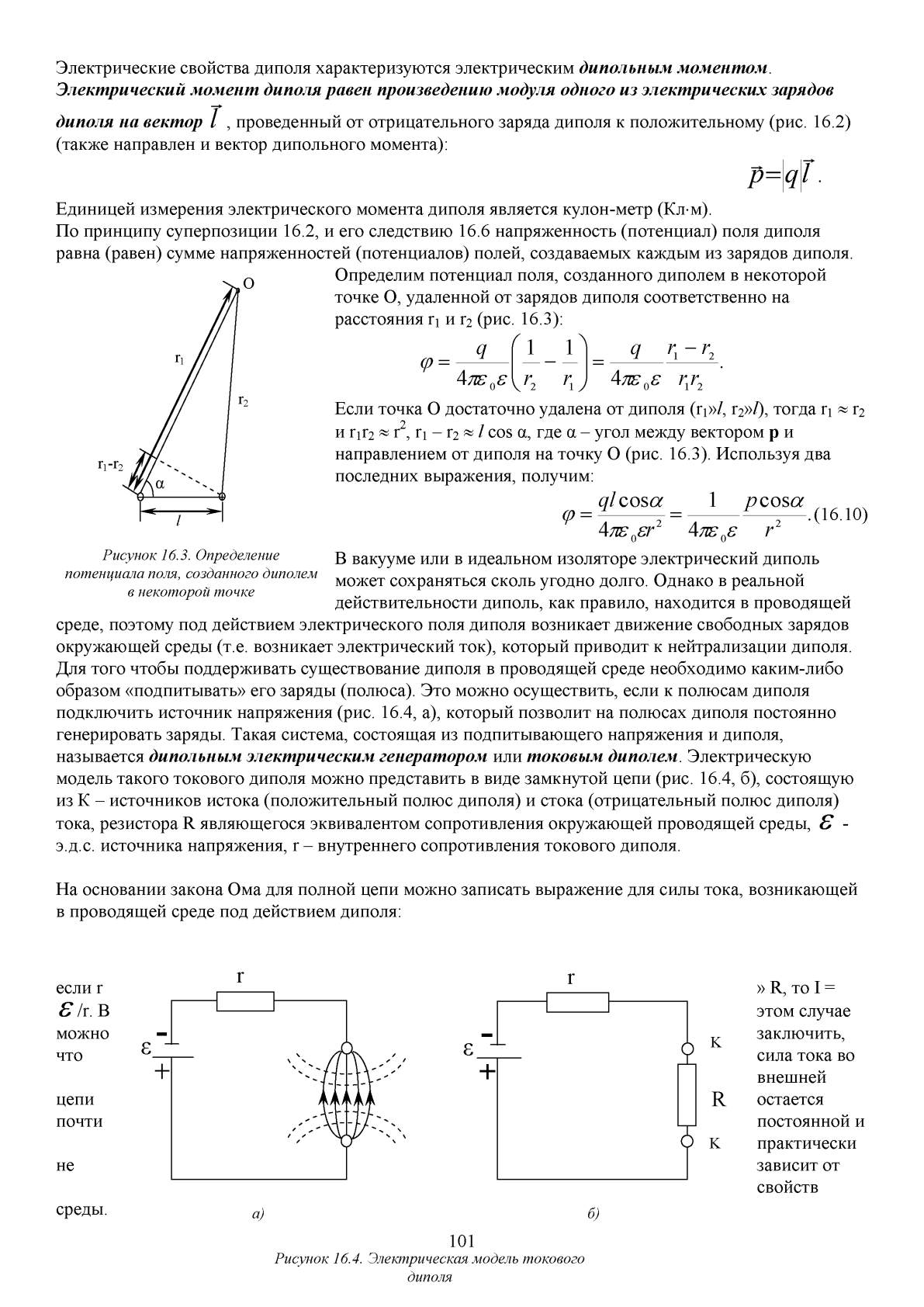
Определим потенциал поля, созданного диполем в некоторой
точке О, удаленной от зарядов диполя соответственно на
расстояния ri и r2 (рис. 16.3):
(р = q
4
т s
1
1
q
' 1
У
4
л е
0
б
r r
' Г 2
Рисунок 16.3. Определение
потенциала поля, созданного диполем
в некоторой точке
Если точка О достаточно удалена от диполя (r1»/, r2»/), тогда r1« r2
и r1r2 « r2, r1- r2 «
/
cos а, где a - угол между вектором р и
направлением от диполя на точку О (рис. 16.3). Используя два
последних выражения, получим:
q l
c o s a
1
p
c o s a
(p = -
--------
z- =
--------- — - 2— . (16.10)
4 m 0sr
4 m
s
r
В вакууме или в идеальном изоляторе электрический диполь
может сохраняться сколь угодно долго. Однако в реальной
действительности диполь, как правило, находится в проводящей
среде, поэтому под действием электрического поля диполя возникает движение свободных зарядов
окружающей среды (т.е. возникает электрический ток), который приводит к нейтрализации диполя.
Для того чтобы поддерживать существование диполя в проводящей среде необходимо каким-либо
образом «подпитывать» его заряды (полюса). Это можно осуществить, если к полюсам диполя
подключить источник напряжения (рис. 16.4, а), который позволит на полюсах диполя постоянно
генерировать заряды. Такая система, состоящая из подпитывающего напряжения и диполя,
называется
дипольным электрическим генератором
или
токовым диполем.
Электрическую
модель такого токового диполя можно представить в виде замкнутой цепи (рис. 16.4, б), состоящую
из К - источников истока (положительный полюс диполя) и стока (отрицательный полюс диполя)
тока, резистора R являющегося эквивалентом сопротивления окружающей проводящей среды,
S
-
э.д.с. источника напряжения, r - внутреннего сопротивления токового диполя.
На основании закона Ома для полной цепи можно записать выражение для силы тока, возникающей
в проводящей среде под действием диполя:
если r
S ir .
В
можно
что
цепи
почти
не
среды.
а)
б)
101
Рисунок 16.4. Электрическая модель токового
диполя
K
R
к
» R, то I =
этом случае
заключить,
сила тока во
внешней
остается
постоянной и
практически
зависит от
свойств
r
r

